1.次の方程式を解きなさい。 (1) (2) (3)6 3(2 5) (4) 1 ( 6) (5) 2 2. についての方程式 の解が であるとき、 の値を求めなさい。 1個 円のりんごと1個 円のなしを合わせて15個買い、 代金の合計を 円にしたい。りんごとなしをそれぞれ何個買えば よいですか。 x+a1 次の方程式を解きなさい。 2x5=9 4x7=1 3x8=5 5x12=3 7x9=19 2x7=13 6x5=13 14x6=15 11=3x4 9=4x7 8=6x1 12=5x2 7=3x13 15=8x11 13=2x35 17=9x19 解説リクエスト 解説リクエストフォーム 問題名 問題番号 mail コメント「1次方程式 基本 レベル1から3」を作りました。分母を払うなどよりもずっと前のレベルからじっくりやるドリルで、移項の練習が中心です。 1ページで3段階全てを練習するようにしてみました。

一元一次方程式應用問題 Shareclass
1 次 方程式 問題
1 次 方程式 問題-19/8/28 3年 2次方程式総合問題Lv3 3(2)図の記号が間違っていました。 19/8/9 3年 1,2年の復習Lv1 2② xの値が2から6まで(誤)→xの値が1から6まで(正) 19/7/29 3年 2乗に比例する関数 変化の割合Lv3 1⑤問題 1/6→1/6, 2(2)答 6→ 72 19/5/8 2 1次方程式のプリント ① 方程式の解(問題) (解答と解説) ② 等式の性質① (問題) (解答と解説) ③ 等式の性質② (問題) (解答と解説) ④ 1次方程式の解き方① (問題) (解答と解説) ⑤ 1次方程式の解き方② (問題) (解答と解説)



99以上1 次方程式文章題 シモネタ
練習問題9 任意の連立2元1次方程式をCramerの公式で解くプログラムを作れ。方程式の各 係数と定数項をキーボードから入力出来るようにし、次の連立方程式を解け。 (4x1 5x2 = 14 8x1 28x2 = 64 (念のための解答x1 = 1, x2 = 2) 52 Gaussの消去法 n元の連立1次方程式は「5次方程式は解けない」ということではない.個々の5次方程式には, x 5 =1 のように解けるものがある. 一般に n 次方程式には複素数の範囲で(重解も数えると) n 個の解が存在する(代数学の基本定理:ガウス). 現在のカテゴリ内記事一覧 中学数学 方程式 基本的な1次方程式、方程式の解と定数(中1) いろいろな1次方程式(かっこを含む、係数が小数、係数が分数)(中1)
問3 3 個の未知数に関する2 個の方程式からなる連立1 次方程式であって,無数の解をもち,さ らに解の自由度が1 となるものを1 つ求めよ. 問4 x0 は連立1 次方程式Ax = b の1 つの解とする.以下の問に答えよ. (i) 方程式Ax = o の任意の解x′ に対して,x0 x1年生の数学, 1次方程式, つまずき克服, 質問への回答 つまづきポイント, 中学生向け, 問題と解説, 文章問題 Posted by タカ よろしければシェアお願いします特に,連立1次方程式は,拡大係数行列を行基本変形することで解く ことができる.理論的にも重要であることから,今後は連立1次方程式 は,拡大係数行列を用いて解いて欲しい. 3 例題 例題1 次の連立1次方程式を解け. x y z= 6 x 2y 2z= 11 2x 3y− 4z= 3
能不能只用係數的加、減、乘、除、開方根就把這些根表示出來(即「根式解」)?很明顯的,方程式 x 5 x 4 x 3 x 2 x1=0 與 x 5 2=0 都有根式解 4 。但是,一般五次方程式是不是有根式解? 十六世紀以來,有許多數學家研究五次一般方程式的根式解問題。1次方程式の文章問題の1つ、代金の問題の解き方とポイントです。 中1の方程式では求める文字が1つしか使えませんが、使い方によってはわからないものが2つある場合でも連立方程式は必要ない場合もあります。 ここは計算ミスを確認 問題 \(f(x)=x^42x^24x8\) とする。 (1) \((x^2t)^2f(x)=(pxq)^2\) がxの恒等式となるような整数t,p,qの値を1組求めよ。 (2) (1)で求めた\(t,p,q\) の値を用いて方程式\((x^2t)^2=(pxq)^2\) を解くことにより、方程式\(f(x)=0\) の解をすべて求めよ。 コメント 簡単に因数分解できない4次方程式を解く問題です。



七年级下 数学实际问题与二元一次方程组题型归纳 含练习题答案 七年级 老杨的博客




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear
例如, n 次方程式 的 n 個根如果是 ,, , ,並且 ,則 很可能是一個很好的預解形, 也可能是一個不壞的預解形, 也是一個預解形(其中任一個 u i 是 a 1,a 2,, a n 的多項式)。 所謂的預解式就是滿足某一預解形的方程式,並且此方程式的求解問題比原來C=1の場合の整数解を1つ求めます. 整数解を方程式に代入しましょう. ↑求めた整数解をx,yに代入 両辺をc倍(今回はc=7なので7倍)します. ↑両辺を7倍 STEP 2 あとは先ほどと同じ手順で解きます.問題の1次不定方程式23x+5y=7から2を引きます.1次方程式 axby=c (1) という形の問題を扱う.(不定方程式の整数解とも呼ばれる.) 中学校以来習ってきたように (1)の形の方程式は xy 平面上の直線を表しており,その直線上の点 (x, y) はすべて方程式 (1)の解となっているから,解は無限にある




完整的題型 完美的解法 全解一元一次方程 每日頭條




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear
数学22章連立二元一次方程式「文字を用いた式」<準備問題①> 組 番 名前 1次の にあてはまる数を求めなさい。 1 3 2次の式を,文字の式の表し方にしたがって書きなさい。 3a=3のとき,次の式の値を求めなさい。 12 (1)5-3a (2) a1次関数 1次関数のグラフ01 1次関数のグラフを描く練習問題です。 1次関数のグラフ02 1次関数のグラフを描く練習問題です。 グラフから1次関数01 グラフを見て1次関数を求める問題です。 1次関数を直線の方程式と言います。 直線(1次関数)上の点の座標01 直線(1次関数)上の点の座標を2講 1次不定方程式(2節 ユークリッド互除法) 問題集3章 整数の性質です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!




01一元一次方程的概念一元一次方程初中数学初一 Youtube




一元一次方程式的應用3 應用問題1 2 解的合理性 Ppt Download
一次方程式 大小関係を表す式 132 1 次の に当てはまる言葉を書きなさい。 不等号を使って数量の関係を表した式を といいます。 { 2 次の数量の関係を不等式で表しなさい。 (1)xの5倍は30より大きい。 x 1連立1次方程式の解法 問題1 1 次の連立方程式の解を求めよ (1) x2y 3z = 1 3x5y 6z = 1 x4y 8z = 1 (2) xy z = 1 x2y 3z = 0 x4y 9z = 0 (3) y 2z = 1 xz = 1 2xy = 1 (4) 3x−y 2z = −2 2x2y −5z = 3 x5y 2z = 6 (5) 3x2y −z = −3 2x−y −2z = 3 一次方程式の文章問題 過不足についての練習問題です。 解説記事はこちら gt;一次方程式の利用問題解き方まとめ スポンサーリンク 目次1 方程式練習問題一次方程式の文章問題~過不足~2 練習問題の解答&解説2




一元一次方程式的應用3 應用問題1 2 解的合理性 Ppt Download




一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download
③ グラフから1次関数の式を求める(問題) (解答と解説) ④ 直線の式の求め方①(問題) (解答と解説) ⑤ 直線の式の求め方②(問題) (解答と解説) ⑥ 2元1次方程式と1次関数①(問題) (解答と解説)




1 次方程式問題 シモネタ



Www Boyo Org Tw Boyo Downloads Category 46 17 11 06 01 36 57 Download 3278 E5 9c 8b E4 B8 Ad E7 94 9f E4 B8 80 E5 Ae 9a E8 A6 81 E6 9c E7 9a 84 E6 87 E7 94 A8 E9 A1 8c E5 9e 8b E4 B8 E9 A1 8c08 E9 80 A3 E7 Ba 8c E6 95 B8 E5 95 8f E9 A1 8c E5 Ad B8 E7 94 9f E7 Start



2



初一 一元一次方程 应用题归类分析 你可以试试




一般 一元一次式 數字易位問題 Youtube



名師課輔網 二元一次方程式題目




基測數學 95v1 單選 一元一次方程式的應用問題 評量專區 均一教育平台




翻轉學習影片 國中 數學 一元一次方程式 應用問題 速度公式
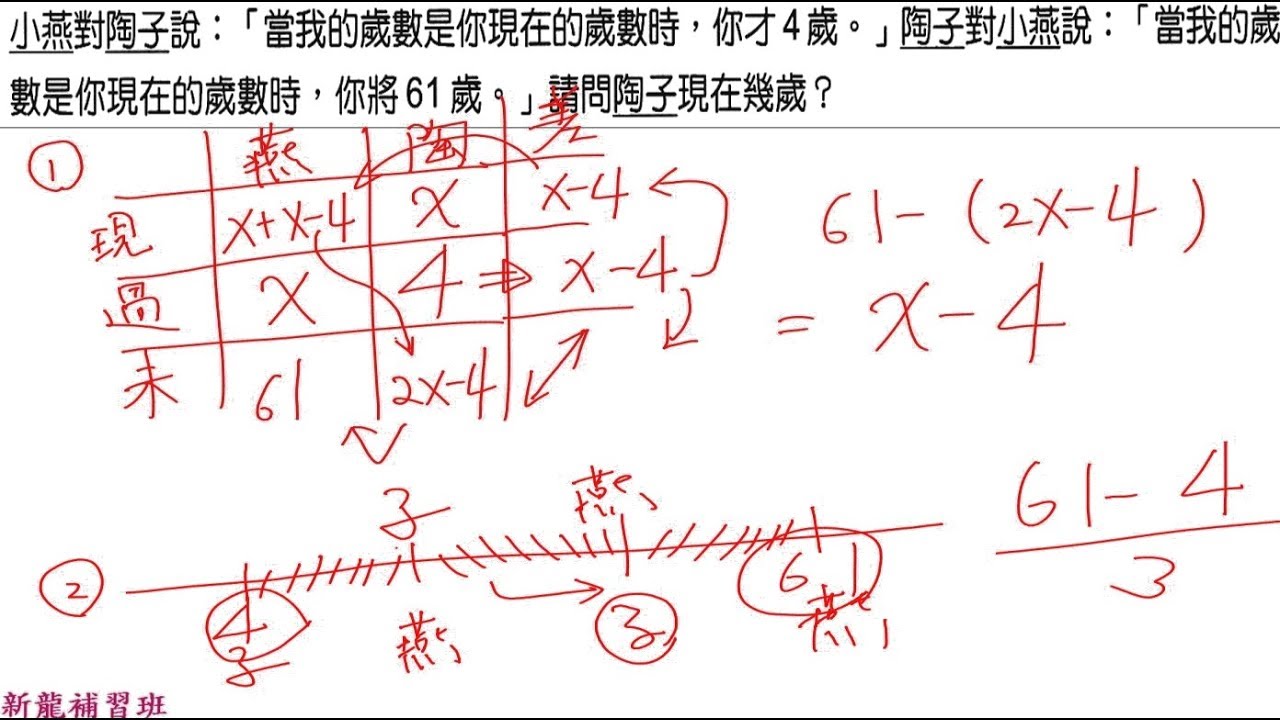



7年級上數學 一元一次方程式 年齡問題 Vs 小學算術解法 17 07 08 Youtube




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




二元一次方程式及其解的意義 Geogebra



Www Camdemy Com Sysdata Users 1 1 Folder 56e5081dff0a15ef Attach e50bdae6bdb6fc9e5cc0 Pdf




一元一次方程应用题 新人首单立减十元 21年8月 淘宝海外



1




二元一次方程式應用問題2 Youtube



幼兒錢幣練習題教材加減乘除應用題台灣外匯 看線圖輕鬆賺外匯




中学数学1年 1次方程式の利用 分配と過不足 受験の月




國中數學的一元一次方程式筆記 Clear




中学数学1年 1次方程式の利用 整数 受験の月




一元一次方程式的解题方法与技巧 自学习网




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear




一元一次方程式應用問題 翰林雲端學院



四年级奥数方程问题 三元一次方程组 四年级奥数题 奥数网




中学数学 一次方程式




二元一次方程組練習題不會 來看看二元一次方程組知識點 每日頭條




一般 一元一次式 倍數問題 Youtube




99以上1 次方程式文章題 シモネタ



初中一元一次方程應用題考試題型大全 考試就這樣考 建議收藏 愛經驗




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




翻轉學習影片 國中 數學 一元一次方程式 應用問題 練習5




解一元一次方程計算題每天訓練 15分鐘 每日頭條




連立3元1次方程式 身勝手な主張




12 一次方程組與行列式 乙




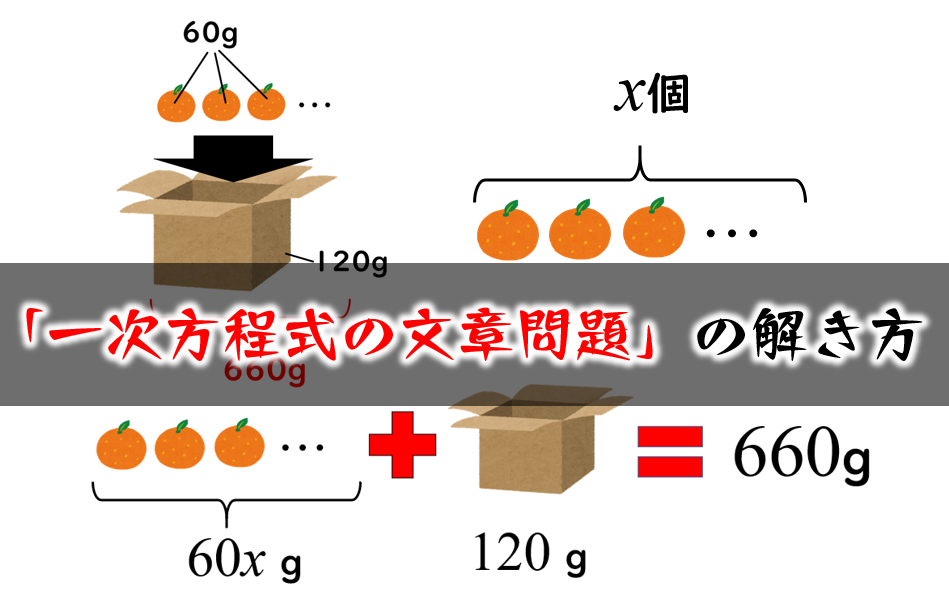
翻轉學習影片 國中 數學 一元一次方程式 一元一次應用問題 一元一次式 裝箱問題
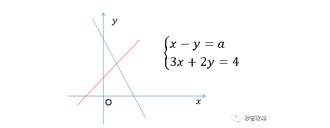



初二数学 函数的思维秒解二元一次方程组问题 看一眼就知道答案 千万别去算 知乎




解一元一次方程計算題每天訓練 15分鐘 每日頭條




均一影片 例題 二元一次方程式 應用問題3 學習單 Shareclass



Www Boyo Org Tw Boyo Downloads Category 46 17 11 06 01 36 57 Download 32 E5 9c 8b E4 B8 Ad E7 94 9f E4 B8 80 E5 Ae 9a E8 A6 81 E6 9c E7 9a 84 E6 87 E7 94 A8 E9 A1 8c E5 9e 8b E4 B8 E9 A1 8c03 E5 B9 B4 E9 A1 E5 95 8f E9 A1 8c E5 Ad B8 E7 94 9f E7




初中数学 一元一次方程常考的13种应用题 掌握考高分 知乎




ベストオブ一次方程式問題集 ぬりえ壁紙hd




2元一次方程式題目初中數學 二元一次方程式 例題2 Gquhm




三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org




一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download




109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass



解一元一次方程50道练习题 经典 强化 带答案 松鼠文库



三元一次方程组测试题 松鼠文库




1 次方程式問題 シモネタ



Ex 二元一次方程組及其解 二元一次聯立方程式 發現學習的美麗新世界




一次方程式の文章題1 数 代金 過不足の問題 無料で使える中学学習プリント




國中數學認識一元一次方程式 Youtube




1次方程式の解き方2 無料で使える中学学習プリント




二元一次方程組練習題不會 來看看二元一次方程組知識點 每日頭條
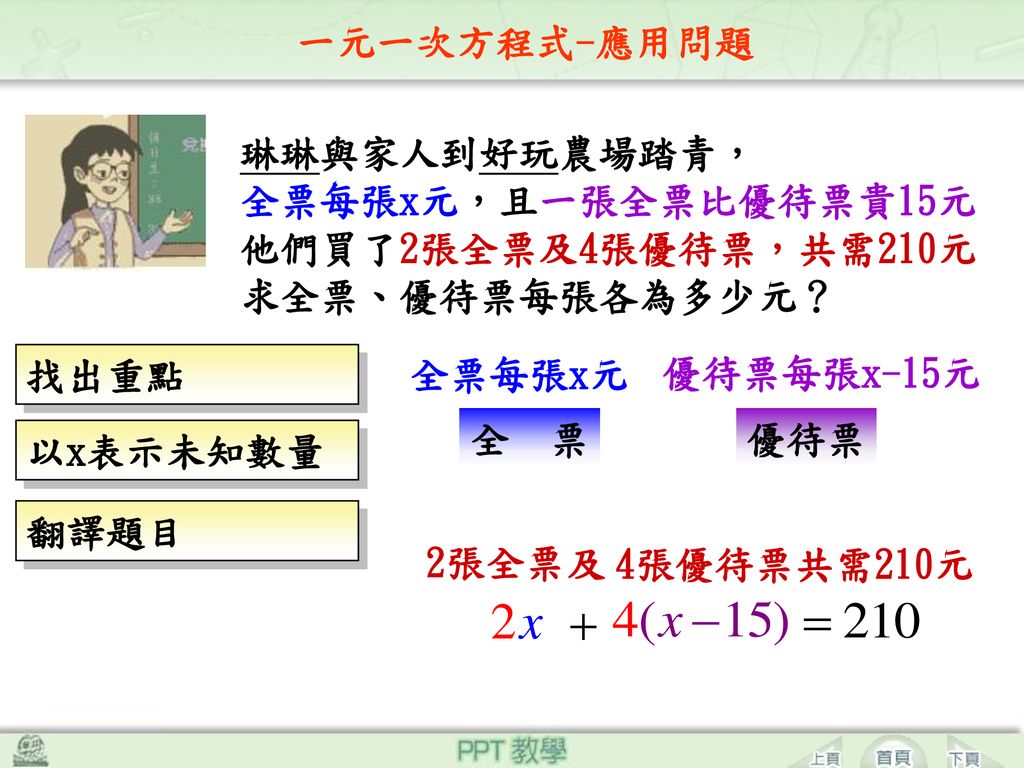



一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download




一次方程式の文章題ー割合に関する問題 無料で使える中学学習プリント




トップ100連立方程式公式 最高のカラーリングのアイデア




一次方程式の解の求め方 数学fun




國中數學總複習 5 一元一次方程式 莫博士 帶你長知識 大师链



Http Web Ntnu Edu Tw Files Single Variable 1st Order Equation Pdf




二次方程式公式解一元二次方程 Ejthgg




一次方程式とは 慶應生が解き方3ステップ教えます 問題 文章題付き 高校生向け受験応援メディア 受験のミカタ




一元一次方程式應用問題 Shareclass




隨筆誌 一上3 3一元一次方程式應用問題 父子年齡等差問題




如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl




一元二次方程式 懶人包



解一元一次方程50道练习题 经典 强化 带答案 松鼠文库




一元一次方程式應用問題 Shareclass



悟空问答 初一学生数学只考了1分 一元一次方程听不懂该怎么办 46个回答




國一數學 一元一次方程式 求幫忙 十分感謝 Clear




隨筆誌 一上3 3一元一次方程式應用問題 一元一次方程式餘數問題



二元一次方程解题时常见思路或方法 掌握后基本都是送分的题目 哔哩哔哩 Bilibili




二元一次聯立方程式的幾何意義 Live 多媒體數學觀念典online



名師課輔網 一元一次方程式應用問題人數




國中數學總複習 6 二元一次聯立方程式 莫博士 帶你長知識 大师链




初中數學重點突破 一元一次方程相關的6類問題 含例題和解析 每日頭條




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



二元一次聯立方程式之應用問題合理性 Live 多媒體數學觀念典online




一元一次方程式應用問題3人數問題 Youtube




方程式の解き方 簡単な問題で 解き方のコツを覚えよう 中学や高校の数学の計算問題



Q Tbn And9gcsm6 Ygdifx7pydebyfkxkcficln0q2usbh7vlhkbagbczf8kws Usqp Cau



1 次方程式問題 シモネタ



解一元一次方程50道练习题 经典 强化 带答案 松鼠文库




中学1年生 数学 無料問題集 一次方程式 おかわりドリル




1 次方程式問題 シモネタ




例題 二元一次方程式 應用問題1 數學 均一教育平台



1




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




Star Lesson 3 3 一元一次方程式 應用題01 考古題解 Youtube




基測數學 91v1 單選12 一元一次方程式打折問題 評量專區 均一教育平台



1




一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download




觀念 一元一次方程式的意義 數學 均一教育平台




國中數學總複習 5 一元一次方程式 莫博士 帶你長知識 大师链
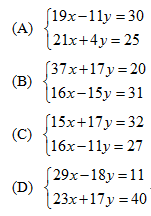



7 X 1 Y 1 為下列哪一個二元一次聯立方程式的解 阿摩線上測驗



七年级数学一元一次方程50道练习题 含答案 侵权



1次方程式で難しい問題を作ってください解説も載せていただけると幸いです文章題 Yahoo 知恵袋




最も共有された 1 次方程式分数 シモネタ



0 件のコメント:
コメントを投稿